本周学习汇报

自然辩证法考试

原型学习综述

Prototypical Networks for Few-shot Learning

Rethinking Semantic Segmentation: A Prototype View

1. 自然辩证法考试

1.1 部分资料整理

1.2 考试题目

2. 关于原型学习

张幸幸, 朱振峰, 赵亚威, 等. 机器学习中原型学习研究进展[J]. 软件学报, 2021: 0-0.

2.1 原型学习目的

• 为消除数据冗余、发现数据结构、提高数据质量,原型学习是一种行之有效的方式.通过寻找一个原型集来表示目标集,以从样本空间进行数据约简,在增强数据可用性的同时,提升机器学习算法的执行效率.
• 数据约简的两种方式
  • 针对特征空间：特征降维、特征选择
  • 针对样本空间：原型生成、原型选择

2.2 原型学习的应用

• 对机器学习而言： 主动学习、自步学习、生成对抗网络、支持向量机、模型压缩
• 对实际应用而言： 计算机视觉、模式识别、图像和自然语言处理、生物医学、传感网络、信息推荐等领域的众多应用
• 对数据处理而言： 数据的快速存储、压缩、生成、清洗、可视化和标注

2.3 原型学习的相关工作

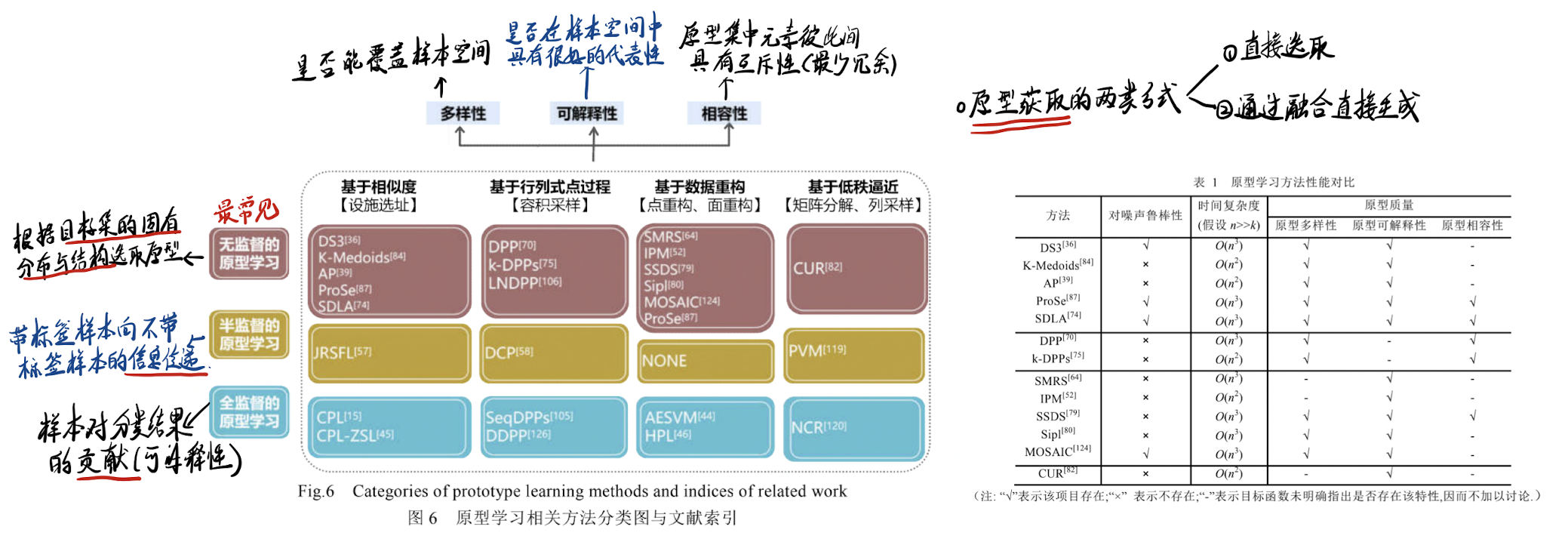
• 主要研究方向： 无监督原型学习。

2.4 原型学习监督方式

2.4.1 无监督原型学习

• 优化： 一个特定的准则，如设施选址、最大边缘相关度、稀疏编码等。
  • 稀疏编码准则： 假定目标数据位于一个或多个子空间中,这样便于将原型选择问题转换为稀疏字典选择问题,并用字典重构误差衡量原型集在目标集中的重要性.
  • 设施选址准则： 一般则是基于给定的成对相似性或相异性,选择编码损失(服务成本)最小的数据点作为原型.其中原型集编码目标集的损失与原型的重要性成反比关系
• 目标： 选取目标数据集中最具代表性的一个子集。

2.4.2 半监督原型学习

• 目标： 了解每个原型的特定类别。
• 方式： 引入一个源集,并将原型选择建模成设施选址问题,但是利用它从目标集中而不是源集中找出代表性样本。
  

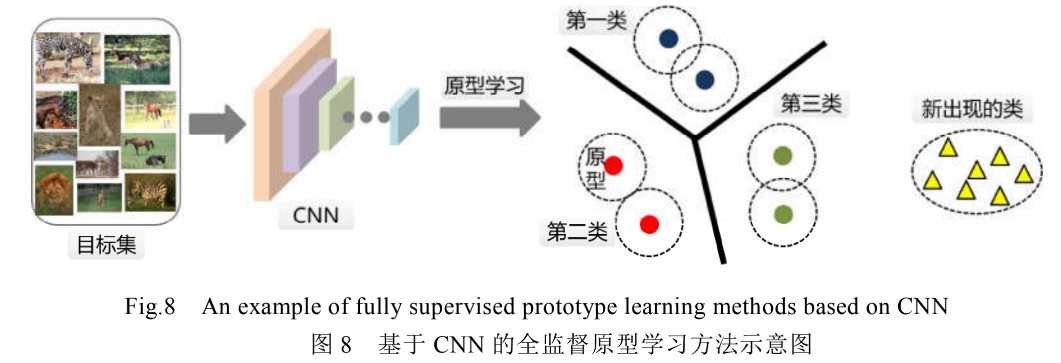
2.4.3 全监督原型学习

• CPL： 通过最大化类内聚集度和类间散度,设计一个基于距离度量的原型损失函数,从而学习目标集中每一类别的数据原型.进而,将测试数据与所有原型做匹配,可以对测试集做出判决,最终实现高精度和强鲁棒的模式分类。

2.5 原型学习相关方法

2.5.1 基于相似度的原型学习

• 方法： 最小化目标集和原型集之间的全局差异。
• K-Medoids $$\min _{\mu_{j} \in Y, r_{i j}} \sum_{i=1}^{n} \sum_{j=1}^{k} r_{i j} D\left(y_{i}, \mu_{j}\right)$$ 其中D代表一种距离测量方式，如欧氏距离。

2.5.2 基于行列式点过程的原型选择

• 目标集上的点模式的概率测度： $$\begin{array}{c} P(\Omega ; L)=\frac{\operatorname{det}\left(L_{\Omega}\right)}{\operatorname{det}(L+I)} \\ \sum_{\Omega \subseteq Y} \operatorname{det}\left(L_{\Omega}\right)=\operatorname{det}(L+I) \end{array}$$
• 可以很好地解决抽样中的互斥性的问题，有利于形成原型集的多样性。

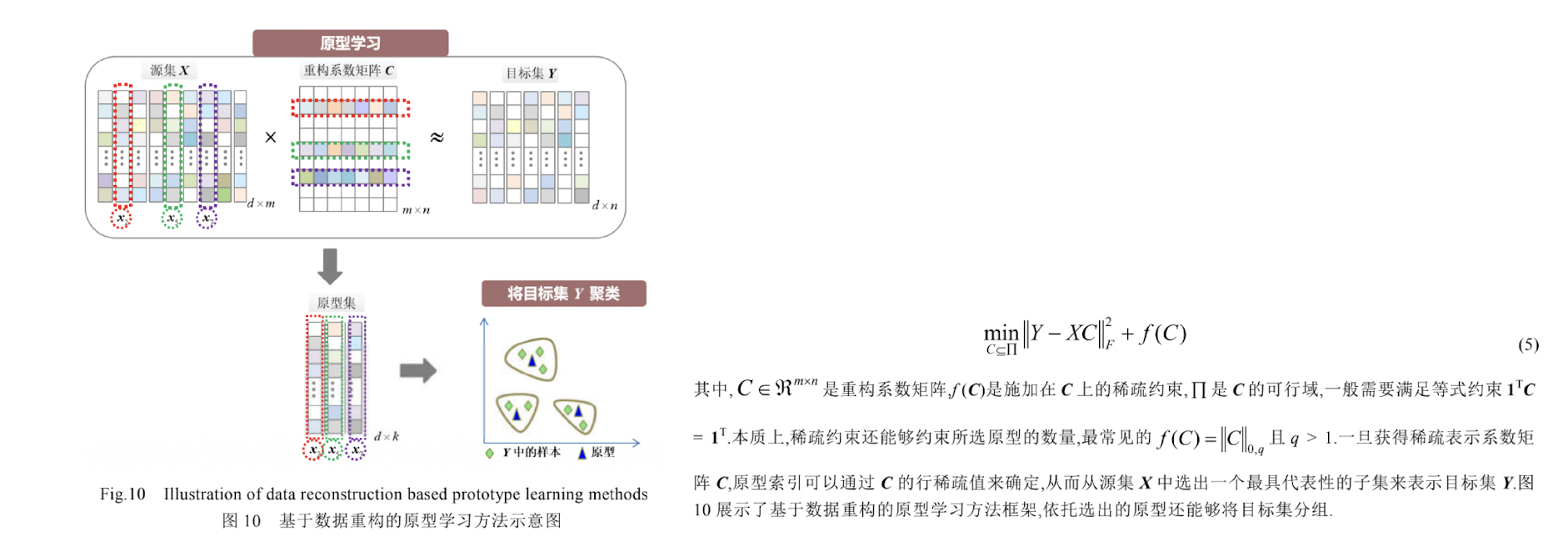
2.5.3 基于数据重构的原型学习

• 方法： 通过最小化原型集重构目标集的残差,来保证原型的可解释性.
  

2.5.4 基于低秩逼近的原型选择

• 思想： 主要思想是通过矩阵分解,并利用随机或贪婪算法来寻找低秩矩阵列的子集,使得目标集矩阵的几行(列)能够近似整个低秩矩阵,而这几行(列)即目标集的原型集.
• CUR 分解的本质 $$\min _{C, U, R}\|Y-C U R\|_{F}^{2}+f(C, R)$$

其中f (C,R)表示施加在矩阵 C 和 R 上的约束,且矩阵 C 由目标集 Y 中的几列组成,而矩阵 R 由目标集 Y 中的几行组成.

2.6 原型学习的未来方向

• 知识迁移驱动的原型生成： 根据其他有标注的样本提升原型学习可利用的信息量。
• 有缺陷数据的原型生成： 给定的目标集数据,通常在底层特征空间和高层语义空间容易出现缺陷。
• 原型分布式学习： 通过最大化利用分步式计算的效能,不仅保护各个工作站的数据信息,同时还可以有效解决传统原型学习算法的准确率与效率无法同时满足的问题。
• 面向深度学习的原型学习： 原型学习方法通过识别信息量最大的训练实例来提高大规模数据集机器学习的数据效率。
• 原型的质量评价体系： 原型学习问题迫切需要一个统一的数据驱动的评价标准,而非任务驱动的评价标准,以精准度量原型的质量,尤其是可解释性、代表性和多样性。

3. 元学习(初步了解)

3.1 题目: 元学习研究综述

论文链接

3.2 内容

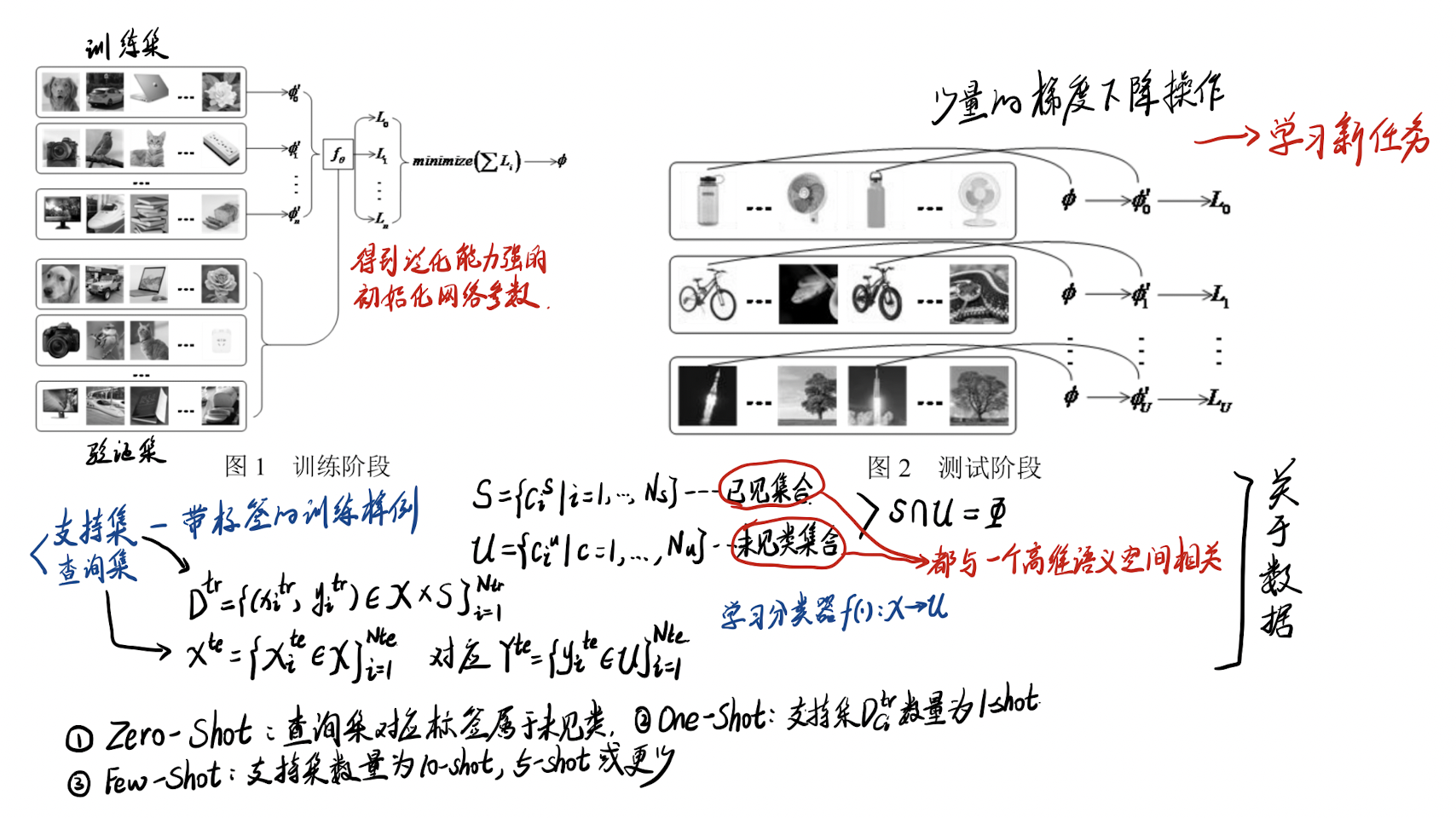
• 提出目的： 针对传统神经网络模型泛化性能不足、对新种类任务适应性较差的特点.元学习的目的就是为了设计一种机器学习模型，这种模型有类似上面提到的人的学习特性，即使用少量样本数据，快速学习新的概念或技能.
• 实例： 小样本学习.
• 主要表现： 提高泛化性能、获取好的初始参数、通过少量计算和新训练数据即可在模型上实现和海量训练数据一样的识别准确度.
• 元学习的三个要求
  • 包含一个学习子系统；
  • 利用以前学习中提取的元知识来获得经验，这些元知识来自单个数据集或不同领域；
  • 动态选择学习偏差.
    

4. 小样本学习的原型网络

Prototypical Networks for Few-shot Learning

/2-Learn Method/2-Meta Learning/2-Prototypical Networks/2017-Prototypical Networks for Few-shot Learning(NIPS).pdf

4.1 Introduction

• Problem: Few-shot classification,a classifier must generalize to new classes not seen in the training set.
• Method: Learn a metric space,computing distances to prototype representations of each class.
• Advantages: they reflect a simpler inductive bias that is beneficial in this limited-data regime, and achieve excellent results.
• Contributions
  • Formulate Prototypical Networks for both the few-shot and zero-shot settings.
  • Draw connections to Matching Networks in the one-shot setting, and analyze the underlying distance function used in the model.
  • Relate Prototypical Networks to clustering in order to justify the use of class means as prototypes when distances are computed with a Bregman divergence, such as squared Euclidean distance.

4.2 Related Work

• Matching Networks: Uses an attention mechanism over a learned embedding of the labeled set of examples (the support set) to predict classes for the unlabeled points (the query set).Matching Networks can be interpreted as a weighted nearest-neighbor classifier applied within an embedding space.

• Meta-Learning: Training an LSTM to produce the updates to a classifier, given an episode, such that it will generalize well to
  a test-set.

4.3 Methodology

4.3.1 Prototypical Networks in the few-shot and zero-shot scenarios.

4.3.2 Training Algorithm

4.4 Experiments

• Quantitative Analysis：
  
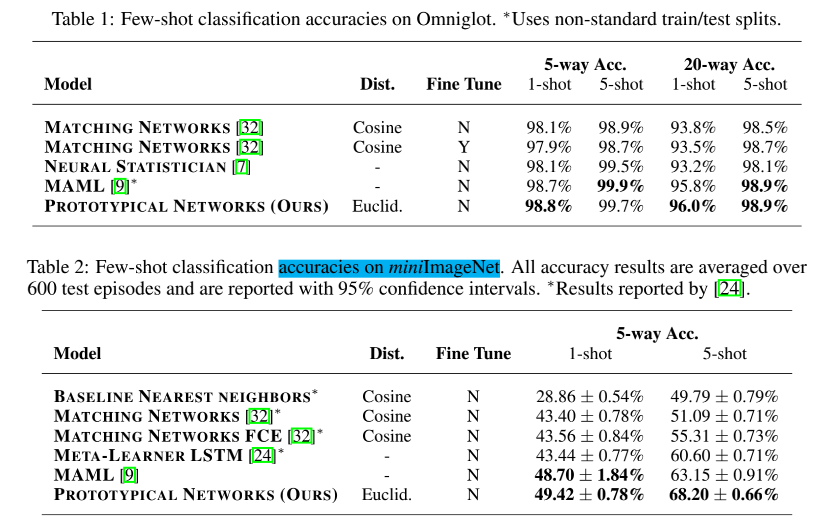
  • Omniglot Few-shot Classification
  • miniImageNet Few-shot Classification
  • CUB Zero-shot Classification

4.5 Conclusion and Future Work

• Prototypical Networks: Few-shot learning based on the idea that we can represent each class by the mean of its examples in a representation space learned by a neural network.
• Achieve state-of-the-art results on the CUB-200 dataset.

5. 原型视图在语义分割中的应用

Rethinking Semantic Segmentation: A Prototype View

GitHub
/6-Segmentation/1-Network/2022-Rethinking Semantic Segmentation- A Prototype View(CVPR oral).pdf

5.1 Introduction

• Parametric Prototype Learning
  • parametric softmax: pixel-wise features for dense prediction.
  • query vectors: utilize a set of learnable vectors to query the dense embeddings for mask prediction.
• Non-Parametric Prototype Learning: This paper.

5.1.1 Questions

A. What are the relation and difference between them(parametric softmax/query vectors )?

• parametric models based on learnable prototypes. Consider a segmentation task with C semantic classes. Most existing efforts seek to directly learn C class-wise prototypes – softmax weights or query vectors – for parametric, pixel-wise classification.

B. If the learnable query vectors indeed implicitly capture some intrinsic properties of data, is there any better way to achieve this?

• more fundamental—>>C&D.

C. What are the limitations of this learnable prototype based parametric paradigm?

• representative ability: insufficient to describe rich intra-class variance. The prototypes are simply learned in a fully parametric manner, without considering their representative ability;
• parameters need: generalizability especially in the large-vocabulary case;
• intra-class compactness: only the relative relations between intra-class and inter-class distances are optimized; the actual distances between pixels and prototypes, i.e., intra-class compactness, are ignored.

D. How to address these limitations?

• Contribution: develop a nonparametric segmentation framework, based on non-learnable prototypes.
• Advantages:
  • each class is abstracted by a set of prototypes, well capturing class-wise characteristics and intra-class variance;
  • due to the nonparametric nature, the generalizability is improved;
  • via prototype-anchored metric learning, the pixel embedding space is shaped as well-structured, benefiting segmentation prediction eventually.
    

5.2 Related Work

• Semantic Segmentation.
• Prototype Learning: Based on the nearest neighbors rule– the earliest prototype learning method.
• Metric Learning: The goal of metric learning is to learn a distance metric/embedding such that similar samples are pulled together and dissimilar samples are pushed away.

5.3 Methodology

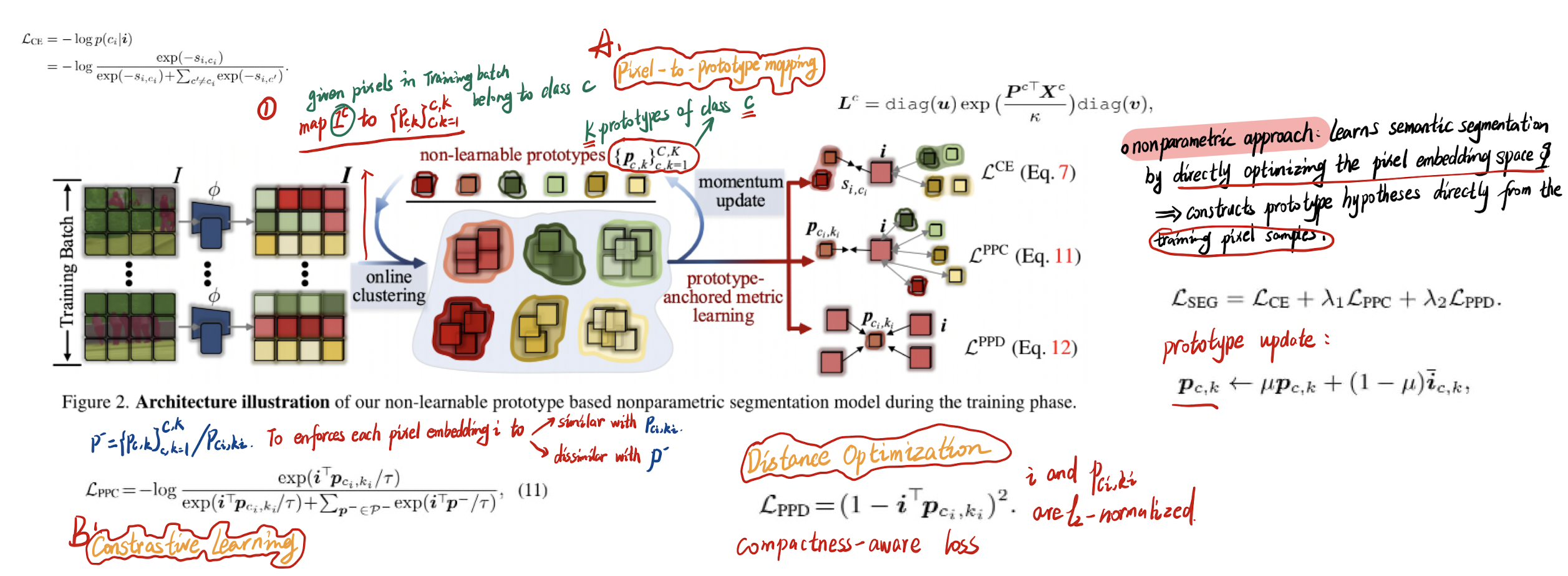
• Non-Learnable Prototype based Pixel Classification
• Within-Class Online Clustering
• Pixel-Prototype Contrastive Learning
• Pixel-Prototype Distance Optimization
• Network Learning and Prototype Update

5.4 Experiments

• Quantitative Analysis：
  

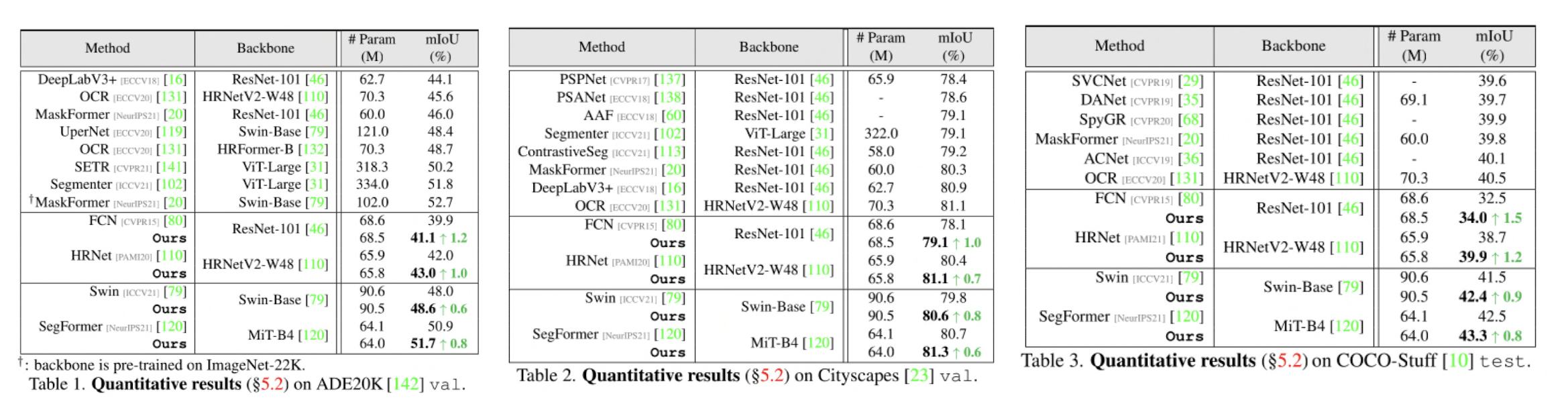
• Qualitative Analysis：
  

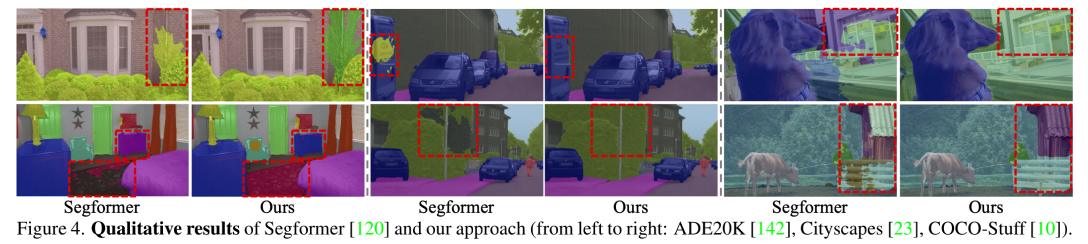
5.5 Conclusion and Future Work

Conclusion

• explicit prototypical representation for class-level statistics modeling;
• better generalization with nonparametric pixel-category prediction;
• direct optimization of the feature embedding space.

Future Work

• directly resemble pixel- or region- level observations.

6. 下一步计划

• 调研扩散模型的一些内容
• 了解元学习和迁移学习的主要思想